Let (X, µ) be a probability space, and let T : X → X be a measure-preserving transformation. If x ∈ X is a point, the basic question that ergodic theory seeks to study is to what extent the orbit of x under iterates of T “equidistributes” in X with respect to the measure µ. This equidistribution is often measured from a function-theoretic perspective: the classical objects of study are the Cesàro averages,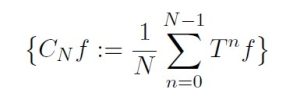
and the fundamental question is to what extent if any {CN f } converge. The two classical ergodic theorems, due to Von Neumann and Birkhoff, dictate that {CN f } converge both in norm and pointwise for f ∈ L2(X).
Once the setting switches from the study of averages of a single function to the multi-linear setting, the difficulty of the problems increases dramatically, and the connections between ergodic theory and other disciplines emerges. These connections were first established in H. Furstenberg’s ergodic theoretic-proof of E. Szemerédi’s theorem on the existence of arbitrarily long arithmetic progressions inside of subsets of integers with positive upper density. In particular, the correspondence principle Furstenberg developed has produced several far reaching extensions of Szemerédi’s theorem to combinatorial number theory, perhaps the most famous of which is the proof of B. Green and T. Tao that the primes contain arbitrarily long arithmetic progressions. On the other hand, combinatorial and number-theoretic considerations have inspired new lines of research in the field of multiple ergodic theory.
Following Furstenberg’s approach, a key step in proving combinatorial Szemeredi-type theorems is an analysis of the limiting behavior of the so-called multiple ergodic averages,
(1)
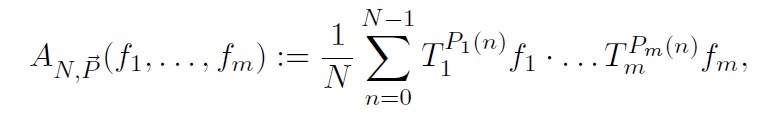
where Ti : X → X are measure-preserving transformations, fi ∈ L∞(X) are bounded functions on a probability space, and Pi : Z → Z are polynomial sequences. For instance, to prove Szemerédi’s Theorem, Furstenberg needed to analyze the limiting behavior of the averages (1) in the case where all polynomials are linear, namely
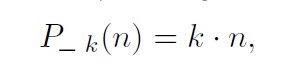
and the convergence in question was convergence in the L2(X)-sense (norm convergence); Furstenberg’s result remained state-of-the-art for more than twenty years.
The first breakthrough in multiple ergodic averages along non-linear polynomial orbits was due to H. Furstenberg and B. Weiss in the 1990s, which lead to a flurry of research, ultimately leading to M. Walsh’s celebrated convergence result, an optimal convergence result in the category of norm convergence of multiple ergodic averages.
Understanding convergence phenomena in the pointwise setting is far more subtle. Indeed, the issue of pointwise convergence of a single function along a polynomial orbit remained open until breakthrough work of Bourgain in the late 1980s and early 1990s; the issue of norm convergence follows from elementary Hilbert space orthogonality arguments.
In recent work with M. Mirek (Rutgers University) and T. Tao (UCLA), I established the first pointwise convergence result in the category of multiple (non-linear) polynomial ergodic averages, namely a pointwise bilinear polynomial ergodic theorem.
The theme of this proposal is to develop the theory of pointwise convergence of multiple polynomial ergodic averages in as close an analogy to Walsh’s result as possible. Although the questions posed are dynamical, results of this line of inquiry will lead to major advances in additive combinatorics, combinatorial number theory, and harmonic analysis.
