Prof. Dr Dennis M. Kochmann
ETH Zurich, Switzerland
Simulations have revolutionised the way we tackle many engineering problems from the nano- to the macroscale. Although we have modelling tools for all scales, we face challenges when problems extend across scales. Atomic-level accuracy at engineering length and time scales is largely out of reach.
As an inexpensive and simple alternative to the experimental testing of prototypes, simulations allow us to approximately predict the behaviour of a device, component, or structure and to infer their mechanical, physical, or chemical properties. With the increase in available computational power and the optimisation of codes and hardware over the past decades, computer simulations have gained tremendous importance. As an example, consider the design of an airplane wing. While the development of the wings for the Boeing 767 (entering service in 1982) required the fabrication and testing of 77 wing prototypes, its younger sibling, the Boeing 787, was designed almost 30 years later based on 11 wing prototypes and 800,000 hours of high-performance computing. Of course, this requires highly accurate, validated, and efficient computational techniques to predict the behaviour of the various structural components and materials of interest.
Materials have always played a key role—long before the word ‘engineering’ was invented. We name the early ages of mankind after the materials that dominated our ability to shape the world: stone, bronze, and iron. The second half of the twentieth century is often referred to as the Silicon Age or Digital Age for the same reason: our lives have been transformed by the emergence of semiconductor-based computer chips—just like our ability to perform complex simulations of material behaviour.
The multiscale nature of materials
Materials are fascinating products of nature with an extremely rich multiscale architecture. Underneath the macroscopic façade of a homogeneous piece of metal, ceramic, or polymer lies an abundant wealth of features at smaller scales, all the way down to the elementary constituents of matter: the atoms and their building blocks. Importantly, it is the sum of all small-scale features, from the sub-nanometre scale of atoms to the micro- or millimetre-scale internal structure of a material, that is responsible for the material’s properties. Its strength, its stiffness, its resilience, its formability, its toughness, or even its visual appearance and its weight—all are macroscopic manifestations of very many small-scale features.
Since the Stone Age, one constant challenge that mankind has faced is the quest to understand, optimise, and, ultimately, design material properties by demand. This requires a fundamental understanding of where material properties originate. Over the centuries, we have learned why brittle materials like stone break easily (because they can accommodate very limited deformation before breaking atomic bonds). We have understood why certain metals can be rolled into thin sheets (because they contain a myriad of small-scale defects that can accommodate large deformation, especially at elevated temperatures). And we have understood why the blacksmith needs to dip the red-hot sword into cold water to harden it (because it freezes the atomic crystal without allowing for significant reconfiguration).
Despite tremendous progress in materials science and related disciplines, especially over the past century, we are still far from accurately predicting a material’s properties based on its small-scale features. Simulations have gained importance since they enable us to simulate material behaviour as an alternative to expensive or intricate experimentation. Yet, predictive simulations have remained a holy grail—and have been the goal of COGRA, a code for COarse-GRAined atomistics (and an ERC COnsolidator GRAnt).
The challenge of scales
The biggest problem arises from the vast range of scales involved. Metallic materials are an example of wide technological importance, which we focus on with COGRA. Atomic spacings are on the order of half a nanometre, and atomic motion occurs of time scales on the order of femtoseconds. Crystal defects in metals, responsible for large permanent deformation, reside on the order of micrometres and move over significantly longer time scales. Most metals are polycrystals made of grains covering the range from hundreds of nanometres to hundreds of micrometres. And most metallic devices (aside from micro- and nanotechnologies) are even larger.
Unfortunately, important phenomena that govern material behaviour extend across all those scales. Take hydrogen embrittlement. When a metal is in contact with a corrosive environment (such as pipelines and pressure vessels), hydrogen atoms diffuse from the environment into the metal and become attracted by crystal defects and, in particular, grain boundaries. Where hydrogen accumulates, it may lead to the formation of pores, voids, and cracks, which ultimately results in material failure under sustained loading. This process is based on the motion of individual atoms over very long times in polycrystals with large grain sizes and abundant defects. Another example is recrystallisation. When a metal is kept at elevated temperature (with or without applied loads), its microstructure tends to evolve slowly over time, accommodated by an atomic-level rearrangement of defects and associated changes to the polycrystalline grain network. Again, the reorganisation of atoms over long times over large distances is responsible.
Bridging across scales
Existing modelling techniques run into a problem when dealing with such scenarios. We have excellent methods to simulate material behaviour at each scale involved: from molecular dynamics (MD) and Density Functional Theory at atomic and sub-atomic scales, respectively, to phase-field methods and discrete dislocation dynamics at the defect level, all the way up to finite-element calculations at engineering scales. However, each of those is applicable to a limited range of length and time scales—none of them is suitable to bridge across all scales, from sub-nanometres to micrometres and from femtoseconds to seconds or even days. For example, the computational costs of MD scale with the number of atoms and the number of time steps to be simulated, which prevents large-scale, long-time simulations. This is where COGRA enters the picture. We combine techniques from engineering mechanics, finite element modelling, statistical mechanics, physics, and computational science into a computational framework able to bridge across length and time scales in crystalline solids. This is achieved primarily by two pillars.
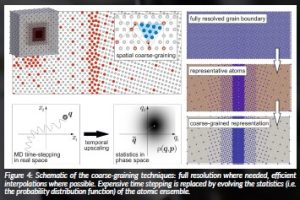
On the one hand, we use spatial coarse-graining based on the quasicontinuum approach to bridge across length scales. The idea is to not simulate every single atom but to concentrate on those atoms that matter. In regions of high interest, e.g. in the vicinity of defects, near grain boundaries or free surfaces, we retain full atomic resolution and simulate every atom. In other regions, away from defects and domains of considerable atomic rearrangement, we simulate only a few atoms, which we deem representative for what happens in their vicinity. We adopt highly-efficient finite-element techniques to interpolate in between representative atoms to infer the physics of all those atoms not modelled explicitly. Importantly, such coarse-graining is solely based on atomic interaction potentials and hence free of other empirical modelling assumptions, proliferating atomic-level accuracy to significantly larger scales. In addition, model adaptivity allows us to automatically track those full-resolution regions of interest during the course of a simulation without any a priori knowledge. Our novel updated-Lagrangian formulation especially allows for the simulation of severe deformation and large atomic rearrangements, applicable primarily to crystalline solids such as metallic materials.
On the other hand, we upscale in time by separating the slow mean motion of atoms from their fast thermal vibrations, which are instead represented by statistical information (using a Gaussian phase packet approximation). This allows us to simulate the slow atomic motion over long times without the need to resolve each and every thermal fluctuation while letting the statistical measures of the vibrations evolve slowly over time. Besides simulating mechanical deformation, such an approach also lends itself to modelling heat and mass transport. These occur at significantly slower scales than atomic vibrations and are of importance when dealing with thermal gradients and diffusion. As a particular challenge, these processes are still not fully understood from a fundamental perspective. Therefore, we also investigate the transport of heat and mass at the atomic level by MD simulations.
Applications
A key benefit of COGRA is its ability to compute equilibrium properties as well as quasistatic processes at finite temperature without the need for resolving thermal vibrations (as commonly done in MD). It can also tackle significantly larger systems than MD (through the aforementioned coarse-graining of the simulation domain). We have successfully applied this framework to study the influence of temperature on interfacial energies, such as the energies of free surfaces (and associated surface elasticity) and grain boundaries in polycrystals. We have studied the motion and interaction of defects in metals, and we are investigating the influence of alloying on the aforementioned scenarios (to tackle a much wider class of metallic materials).
Our primary applications for COGRA are hydrogen embrittlement in iron and recrystallisation in magnesium. Hydrogen embrittlement and the related corrosion cracking are threats to the lifetime of engineering structures and require the long-term observation of atomic-level mass transport and mechanical degradation at finite temperature. Hydrogen storage, though not our target, is a related problem with similar challenges. Magnesium (Mg) is a promising structural metal due to its high strength-to-weight ratio (being ca. 50 per cent lighter than aluminium) and its abundance in the Earth’s crust. Recrystallisation occurs, e.g. during annealing and severe plastic deformation, both being important steps in thermomechanical processing of Mg and Mg alloys.
Despite these concrete applications, the framework is sufficiently general to be applied to a variety of problems bridging across scales in crystalline materials. COGRA is being prepared for public release, so the research community will be able to leverage its capabilities in the future (once development, validation, performance optimisation, and benchmarking are complete).
PROJECT SUMMARY
COGRA aims for new simulation techniques to bridge the gap between the accuracy of atomistic simulations and the length and time scales of engineering applications. Combining methods from engineering mechanics, statistical mechanics, materials science, and computational science, the new high-performance framework is used to investigate scale-bridging material processes ranging from metal processing to material failure.
PROJECT PARTNERS
The project is carried out in collaboration with Prof. Prateek Gupta of IIT Delhi and with Prof. Michael Ortiz of the California Institute of Technology, as well as research groups in Germany, Spain, and the US.
PROJECT LEAD PROFILE
Dennis M. Kochmann is Professor of Mechanics and Materials in ETH Zurich’s Department of Mechanical and Process Engineering. He received his education at Ruhr-University Bochum and at the University of Wisconsin-Madison, was a postdoctoral associate at Wisconsin, and Professor of Aerospace at the California Institute of Technology, before joining ETH Zurich in 2017. His research at the crossroads of engineering mechanics, materials science, physics, and numerical methods has been recognised by a number of awards and featured in conference plenary lectures.
PROJECT CONTACTS
Prof. Dr Dennis M. Kochmann
ETH Zurich,
Leonhardstrasse 21
8092 Zürich
Switzerland
mm.ethz.ch/research-overview/coarse-grained-atomistics.html
FUNDING
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 770754.
Figure 1: Length and time scales involved in simulating material behaviour.
Figure 2: Challenges across scales: hydrogen embrittlement is a threat to metals in corrosive environments; recrystallisation occurs during metal processing at elevated temperatures.
Figure 3: Coarse-graining an atomistic system, illustrated for a polycrystal. Simulations use full atomistic resolution near grain boundaries while using an efficiently coarsened description within grains.
Figure 4: Schematic of the coarse-graining techniques: full resolution where needed, efficient interpolations where possible. Expensive time stepping is replaced by evolving the statistics (i.e. the probability distribution function) of the atomic ensemble.
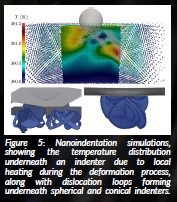
Figure 5: Nanoindentation simulations, showing the temperature distribution underneath an indenter due to local heating during the deformation process, along with dislocation loops forming underneath spherical and conical indenters.