Recent years have seen a boom in the application of statistical and machine learning methods in science and in our everyday life. But to what extent can we rely on them? My ERC project, BigBayesUQ, aims to derive theoretical guarantees and limitations for modern learning approaches in complex mathematical models.
Real-world phenomena are often described by complex mathematical models. For example, in astronomy, the path of light from distant galaxies to us is described by complex mathematical formulas (PDE systems), which can then be used to understand how fast the universe is expanding or the proportion of dark matter in the universe. As another example, novel image recognition methods are being developed for self-driving cars. The observed data are, however, never perfectly clean or accurate, often containing measurement and other errors making the analysis even more difficult. Statistics is the science of analysing and interpreting such noisy, imperfect data, and it plays a leading role in all modern data-centric developments.
In recent years the amount of available information has increased substantially, and the models describing real-world phenomena are becoming increasingly complex. These introduce new challenges for scientists since, despite the ever-increasing power of computers, the computational complexity in certain fields of applications has become overly large, making it impractical or even impossible to carry them out in a reasonable amount of time (or memory requirement).
Protecting the privacy of individuals is also becoming more pronounced. Therefore, novel, modern statistical and machine learning methods are continuously developed to speed up computation using simplified models and computational shortcuts. However, these methods are often used as black-box procedures without rigorous mathematical understanding. This could result in misleading and wrong answers without us even realising it. A particular example is neural networks, with state-of-the-art approaches for image classification with applications ranging from medical imaging to self-driving cars. However, it was shown that minor changes in the input images, which couldn’t even be detected by human eyes (Chatel, 2019), or unusual positions of the objects (Alcorn et al., 2019) could result in completely inaccurate classifications leading to wrong diagnosis or incorrect detection of objects. One essential aspect is understanding how much we can rely on the derived results. In more formal terminology, it is necessary to correctly assess the uncertainty of the procedure, which is based on noisy, real-world data, so can never be perfect.
A principled way of obtaining uncertainty quantification is by using Bayesian methods. Bayesian statistics provides a natural way of incorporating expert knowledge into the model in a probabilistic way. More concretely, based on experience, the expert can assess that certain parameter values are more likely than others. This probabilistic interpretation can be formalised by introducing a prior distribution representing the initial belief of the user. Then, after observing the data, this belief is updated by the new information resulting in the so-called posterior distribution, which presents a more accurate description of the problem driven by the data. This probabilistic statement about the likeliness of the parameter values in the model provides a natural way of quantifying the uncertainty of the procedure.
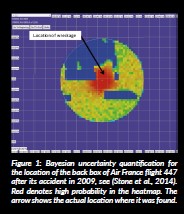
Bayesian statistics is becoming increasingly popular in a wide range of applications, including epidemiology, astronomy, environmental and earth sciences, machine learning and artificial intelligence. For a concrete example, in natural language processing, chatbots provide a list of the most likely next word in a text and choose from them randomly (Naïve Bayes classifier algorithm). Or a Bayesian approach was used to find the black box of the crashed Air France flight 447 (Chatel, 2019) after all other standard approaches failed (see Figure 1).
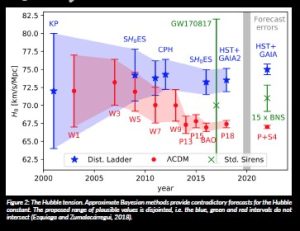
However, Bayesian methods for complex, high-dimensional, large data sets are (typically) computationally very demanding. This has given rise to various approximation approaches to speed up the procedure. These methods trade off accuracy to gain computational efficiency. Yet they typically have very limited theoretical underpinning; hence we cannot know if they are working properly. It has been shown, empirically and theoretically, that many of them can provide overconfident and wrong results. For instance, it was pointed out by Ezquiaga and Zumalacárregui (2018) that using different scalable Bayesian methods (corresponding to different astronomical models) can result in contradictory estimations for the Hubble constant (describing the expansion rate of the universe), as shown in Figure 2.
Whether the applied statistical techniques or the underlying astronomical models were incorrect is unclear. To answer such questions and to reliably use approximate Bayesian methods in a wide range of applications, it is essential to understand their theoretical behaviour. My research focuses on the mathematical description of such modern statistical and machine learning methods (with a particular focus on Bayesian statistical approaches) in the context of mathematical models motivated by real-world applications. I will investigate two state-of-the-art approaches: distributed (parallel) computing and variational inference methods.
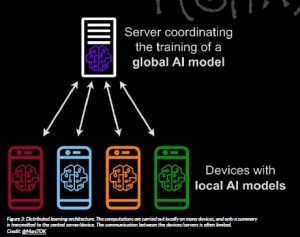
In distributed computational architectures, the data are split amongst different cores/machines and computations are carried out locally, in parallel to each other. The outcomes of these local computations are transmitted to a central core/machine, where they are aggregated into a final result; see Figure 3 for a schematic representation. The computational bottleneck of such approaches is typically the communication between the servers; hence, the information transmission is restricted to make them computationally attractive. Besides the straightforward computational and data storage advantages, distributed methods can be used for privacy protection where storing all sensitive data in a central database (e.g. medical or financial information) is undesirable. Although these methods were extensively studied in the computer science and electrical engineering literature, the focus has been mainly on simple, low dimensional models, and we have scarcely any theoretical understanding of these methods in more complex, modern statistical problems, for some first results and references therein see (Szabo and Zanten, 2019). One particularly important and increasingly popular problem is federated learning, where the machine learning models are trained in a decentralised fashion considering specific network topologies.
The variational Bayesian method approximates the complex posterior by a simpler probability distribution. This simple distribution is chosen from a pre-specified set of distributions using optimisation approaches. There is a clear trade-off in the procedure. On the one hand, a smaller set of possible distributions will speed up the optimisation method and make the model easier to interpret. Still, on the other hand, it will provide less accurate approximations. Variational Bayesian methods are routinely used in all fields of science; for instance, Bayesian deep learning or real-time image segmentation and classification wouldn’t be possible due to the high computational costs without applying variational methods. To understand how much we can rely on the variational method, we have to quantify the information loss occurring in this approximation procedure (Ray and Szabo, 2022).
Understanding the theoretical (mathematical) properties of these state-of-the-art approaches provides us with a principled way of further improving their accuracy and eventually relying on the derived results. The main focus of my work is on mathematical statistics and its intersection with machine learning, information theory and numerical analysis. The investigated theoretical questions are emerging from practice, and occasionally I am also involved in concrete applied projects. I work closely with scientists at the Psychology Institute of Leiden University on developing machine learning methods for the early detection of Alzheimer’s disease (see a more detailed description in the following paragraph), and I am in contact with researchers at Leiden Observatory aiming to develop new statistical tools for understanding and answering fundamental questions in astronomy.
In medical research, different data types are collected and combined to provide the best diagnosis. For instance, for early diagnosis of Alzheimer’s disease, structural and functional MRI data, questionnaire data, EEG data, genetic data, metabolomics data,… etc. can be collected. These data are substantially different both in overall size and quality. To achieve the most accurate early diagnosis, one should find the most important features in these data sets and combine them in an optimal way. Furthermore, since these diagnostic tools can be expensive and of limited capacity, selecting the most relevant ones is important to achieve a reliable, accurate and cost-effective diagnostic method. We have developed a learning approach called stacked penalised logistic regression (StaPLR), which selects the most relevant diagnostic tools and the corresponding most relevant features for predicting to early onset of dementia. This method was successfully applied to clinical data containing patients with Alzheimer’s disease and a control group (van Loon et al., 2022).
References
Alcorn, M. A., Li, Q., Gong, Z., Wang, C., Mai, L., Ku, W-S. and Nguyen, A. (2019) ‘Strike (with) a pose: Neural networks are easily fooled by strange poses of familiar objects’, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Long Beach, California, 15–20 June 2019.
Chatel, G. (2019) Adversarial examples in deep learning. Available at: https://www.mlsecurity.ai/post/adversarial-examples-in-deep-learning.
Ezquiaga, J. M. and Zumalacárregui, M. (2018) ‘Dark Energy in Light of Multi-Messenger Gravitational-Wave Astronomy’, Frontiers in Astronomy and Space Sciences, 5. doi: 10.3389/fspas.2018.00044.
Ray, K. and Szabo, B. T. (2022) ‘Variational Bayes for high-dimensional linear regression with sparse priors’, Journal of the American Statistical Association, 117(539), pp. 1270–1281. doi: 10.1080/01621459.2020.1847121.
Stone, L. D., Keller, C. M., Kratzke, T. M. and Strump, J. P. (2014) ‘Search for the wreckage of air france flight af 447’, Statistical Science, 29(1), pp. 69–80. doi: 10.1214/13-STS420.
Szabo, B. T. and van Zanten, J. H. (2019) An asymptotic analysis of distributed nonparametric methods’, Journal of Machine Learning Research, 20, pp. 1–30. doi: 10.48550/arXiv.1711.03149.
van Loon, W., de Vos, F., Fokkema, M., Szabo, B., Koini, M., Schmidt, M. and de Rooij, M. (2022) ‘Analyzing hierarchical multi-view MRI data with StaPLR: An application to Alzheimer’s disease classification’, Frontiers in Neuroscience, section Brain Imaging Methods, 16. doi: 10.3389/fnins.2022.830630.
Project name
BigBayesUQ
Project summary
New machine- and statistical learning methods are being developed to process the ever-increasing amount of available information. However, these methods often behave like black-box procedures without any theoretical underpinning. In this project, I will derive theoretical guarantees but also limitations of such procedures and, based on their mathematical understanding, increase their accuracy in complex models.
Project lead profile
Botond Szabo is an associate professor at the Department of Data Sciences at Bocconi University and a fellow of BIDSA. He serves as an associate editor of Annals of Statistics and Bayesian Analysis, was a programme chair of the International Society of Bayesian Analysis (ISBA) and the chair of the Scientific Committee of the bi-annual ISBA World Meeting 2022 in Montreal. His research focuses on the theoretical understanding of Bayesian high- and infinite-dimensional methods, scalable statistical and machine-learning approaches and statistical inverse problems. Occasionally he is also involved in applied projects in health sciences, astronomy and combustion kinetics.
Project contact
Botond Szabo
Department of Decision Sciences
Bocconi University
20136, via Rontgen 1, Milano, Italy
www.botondszabo.com
Funding
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation programme under grant agreement No.101041064.